Pythran: Static Compilation of Parallel Scientific Kernels

a.k.a. Python/Numpy compiler for the mass

Proudly made in Namek by serge-sans-paille & pbrunet

`/me`

Serge « sans paille » Guelton

$ whoami
sguelton

R&D engineer at QuarksLab on compilation for security
Associate researcher at Télécom Bretagne
Soldier of fortune

Pythran in a snake shell

A Numpy-centric Python-to-NativeCode translator
A Python code optimizer
A Pythonic C++ library

Core concepts

Focus on high-level constructs
Generate ~~clean~~ high level code
Optimize Python code before generated code
Generate GIl-free, Python-free code
Vectorization and Parallelism
Test, test, test
Bench, bench, bench

Ask StackOverflow

when you're looking for test cases
http://stackoverflow.com/[...]numba-or-cython-acceleration-in-reaction-diffusion-algorithm

import numpy as np
def GrayScott(counts, Du, Dv, F, k):
    n = 300
    U = np.zeros((n+2,n+2), dtype=np.float32)
    V = np.zeros((n+2,n+2), dtype=np.float32)
    u, v = U[1:-1,1:-1], V[1:-1,1:-1]

    r = 20
    u[:] = 1.0
    U[n/2-r:n/2+r,n/2-r:n/2+r] = 0.50
    V[n/2-r:n/2+r,n/2-r:n/2+r] = 0.25
    u += 0.15*np.random.random((n,n))
    v += 0.15*np.random.random((n,n))

    for i in range(counts):
        Lu = (                 U[0:-2,1:-1] +
              U[1:-1,0:-2] - 4*U[1:-1,1:-1] + U[1:-1,2:] +
                               U[2:  ,1:-1] )
        Lv = (                 V[0:-2,1:-1] +
              V[1:-1,0:-2] - 4*V[1:-1,1:-1] + V[1:-1,2:] +
                               V[2:  ,1:-1] )
        uvv = u*v*v
        u += Du*Lu - uvv + F*(1 - u)
        v += Dv*Lv + uvv - (F + k)*v

    return V

Thread Summary

OP: My code is slow with Cython and Numba
Best Answer: You need to make all loops explicit

Cython Version

cimport cython
import numpy as np
cimport numpy as np

cpdef cythonGrayScott(int counts, double Du, double Dv, double F, double k):
    cdef int n = 300
    cdef np.ndarray U = np.zeros((n+2,n+2), dtype=np.float_)
    cdef np.ndarray V = np.zeros((n+2,n+2), dtype=np.float_)
    cdef np.ndarray u = U[1:-1,1:-1]
    cdef np.ndarray v = V[1:-1,1:-1]

    cdef int r = 20
    u[:] = 1.0
    U[n/2-r:n/2+r,n/2-r:n/2+r] = 0.50
    V[n/2-r:n/2+r,n/2-r:n/2+r] = 0.25
    u += 0.15*np.random.random((n,n))
    v += 0.15*np.random.random((n,n))

    cdef np.ndarray Lu = np.zeros_like(u)
    cdef np.ndarray Lv = np.zeros_like(v)
    cdef int i, c, r1, c1, r2, c2
    cdef double uvv

    cdef double[:, ::1] bU = U
    cdef double[:, ::1] bV = V
    cdef double[:, ::1] bLu = Lu
    cdef double[:, ::1] bLv = Lv

    for i in range(counts):
        for r in range(n):
            r1 = r + 1
            r2 = r + 2
            for c in range(n):
                c1 = c + 1
                c2 = c + 2
                bLu[r,c] = bU[r1,c2] + bU[r1,c] + bU[r2,c1] + bU[r,c1] - 4*bU[r1,c1]
                bLv[r,c] = bV[r1,c2] + bV[r1,c] + bV[r2,c1] + bV[r,c1] - 4*bV[r1,c1]

        for r in range(n):
            r1 = r + 1
            for c in range(n):
                c1 = c + 1
                uvv = bU[r1,c1]*bV[r1,c1]*bV[r1,c1]
                bU[r1,c1] += Du*bLu[r,c] - uvv + F*(1 - bU[r1,c1])
                bV[r1,c1] += Dv*bLv[r,c] + uvv - (F + k)*bV[r1,c1]

    return V

Pythran version

Add this line to the original kernel:

#pythran export GrayScott(int, float, float, float, float)

Timings

$ python -m perf timeit -s 'from grayscott import GrayScott' 'GrayScott(40, 0.16, 0.08, 0.04, 0.06)'
Median +- std dev: 108 ms +- 2 ms
$ cython grayscott.pyx
$ clang grayscott.c `python-config --cflags --libs` -shared -fPIC -o grayscott.so -Ofast -march=native
$ python -m perf timeit -s 'from grayscott import GrayScott' 'GrayScott(40, 0.16, 0.08, 0.04, 0.06)'
Median +- std dev: 23.9 ms +- 0.3 ms
$ pythran grayscott.py -Ofast -march=native  # using same clang as backend
$ python -m perf timeit -s 'from grayscott import GrayScott' 'GrayScott(40, 0.16, 0.08, 0.04, 0.06)'
Median +- std dev: 12.9 ms +- 1.6 ms

Beware of Benchmarks(BoB)

GCC 6.3 Timings

$ gcc grayscott.c `python-config --cflags --libs` -shared -fPIC -o grayscott.so -O3 -march=native
$ python -m perf timeit -s 'from grayscott import GrayScott' 'GrayScott(40, 0.16, 0.08, 0.04, 0.06)'
Median +- std dev: 26.4 ms +- 0.5 ms
$ CXX=g++ CC=gcc pythran grayscott.py -Ofast -march=native
$ python -m perf timeit -s 'from grayscott import GrayScott' 'GrayScott(40, 0.16, 0.08, 0.04, 0.06)'
Median +- std dev: 37.4 ms +- 0.5 ms

Lessons learnt

Explicit is not always better than implicit
Many ``optimization hints'' can be deduced by the compiler
High level constructs carry valuable informations
Each compiler has its strenghts

I am not saying Cython is bad. Cython does a great job. It is just pragmatic where Pythran is idealist

Compilation Challenges

u = U[1:-1,1:-1]
U[n/2-r:n/2+r,n/2-r:n/2+r] = 0.50
u += 0.15*np.random.random((n,n))

Array views
Value broadcasting
Temporary arrays creation
Extended slices composition
Numpy API calls

Optimization Opportunities

Lu = (U[0:-2,1:-1] + U[1:-1,0:-2]
  - 4*U[1:-1,1:-1] + U[1:-1,2:] + U[2:  ,1:-1])

Many useless temporaries
Lu could be forward-substituted
SIMD instruction generation opportunities
Parallel loop opportunities

Pythran Usage

$ pythran --help
usage: pythran [-h] [-o OUTPUT_FILE] [-E] [-e] [-f flag] [-v] [-p pass]
               [-m machine] [-I include_dir] [-L ldflags]
               [-D macro_definition] [-O level] [-g]
               input_file

pythran: a python to C++ compiler

positional arguments:
  input_file           the pythran module to compile, either a .py or a .cpp
                       file

optional arguments:
  -h, --help           show this help message and exit
  -o OUTPUT_FILE       path to generated file
  -E                   only run the translator, do not compile
  -e                   similar to -E, but does not generate python glue
  -f flag              any compiler switch relevant to the underlying C++
                       compiler
  -v                   be verbose
  -p pass              any pythran optimization to apply before code
                       generation
  -m machine           any machine flag relevant to the underlying C++
                       compiler
  -I include_dir       any include dir relevant to the underlying C++ compiler
  -L ldflags           any search dir relevant to the linker
  -D macro_definition  any macro definition relevant to the underlying C++
                       compiler
  -O level             any optimization level relevant to the underlying C++
                       compiler
  -g                   any debug level relevant to the underlying C++ compiler

It's a megablast!

Sample Usage

$ pythran input.py # generates input.so
$ pythran input.py -E # generates input.cpp
$ pythran input.py -O3 -fopenmp # parallel!
$ pythran input.py -march=native -Ofast # Esod Mumixam !

Type Annotations

Only for exported functions

#pythran export foo0()
#pythran export foo1(int)

#pythran export foo2(float32[][])
#pythran export foo2(float64[][])
#pythran export foo2(int8[][][])

#pythran export foo3((int, float), int list, str:str dict)

Extra Type Annotations

Combine several signatures in one

#pythran export foo0(int or str)
#pythran export foo3(float32[][] or float32[], int or None)

Extern Type Annotations

foo.pythran file as a companion of foo.py

foo0()
foo1(int)
foo2(float32[][])
foo2(float64[][])
foo2(int8[][][])
foo3((int, float), int list, str:str dict)

Pythran Compilation Flow

Front End

100% based on the gast module
Supports
- Several standard module (incl. partial Numpy)
- Polymorphic functions
- ndarray, list, tuple, dict, str, int, long, float
- Named parameters, default arguments
- Generators…
Does not Support
- Non-implicitly typed code
- Non-const Global variable
- Most Python modules (no CPython mode!)
- User-defined classes…

Middle End

Iteratively applies high level, Python-aware optimizations:

Interprocedural Constant Folding
For-Based-Loop Unrolling
Forward Substitution
Instruction Selection
Deforestation
Scalar Renaming
Dead Code Elimination

Fun Facts: can evaluate pure functions at compile time ☺

Back Ends

Python Back End

Useful for debugging!

C++11 Back End

C++11 implementation of __builtin__ numpy itertools…
Lazy evaluation through Expression Templates
Relies on OpenMP and boost::simd for the parallelization / vectorization

C++11: Typing

the W.T.F. slide

Pythran translates Python implicitly statically typed polymorphic code into C++ meta-programs that are instanciated for the user-given types, and specialize them for the target architecture

In case of errors, it performes some fuzzy type inference to produce a decent error message

C++11: Parallelism

Implicit

Array operations and several numpy functions are written using OpenMP and Boost.simd

Explicit

OpenMP 3 support, ported to Python

#omp parallel for reduction(+:r)
for i, v in enumerate(l):
    r += i * v

OpenMP Extra

Supports

Atomic clause
Critical clause
Task clause
libomp through a custom import omp

Trickz #0

Cython coupling

Cython version 0.26

# cython: np_pythran=True
import numpy as np
cimport numpy as cnp

def diffuse_numpy(cnp.ndarray[double, ndim=2] u, int N):
    cdef cnp.ndarray[double, ndim=2] temp = np.zeros_like(u)
    mu = 0.1

    for n in range(N):
        temp[1:-1, 1:-1] = u[1:-1, 1:-1] + mu * (
            u[2:, 1:-1] - 2L * u[1:-1, 1:-1] + u[0:-2, 1:-1] +
            u[1:-1, 2:] - 2L * u[1:-1, 1:-1] + u[1:-1, 0:-2])
        u[:, :] = temp[:, :]
        temp[:, :] = 0.0

Thanks to Adrien Guinet & OpenDreamKit!

Trickz #1

Generate pure c++ code

$ pythran -e input.py

No Python conversion code, C-API handling etc
Very under-tested
Started as a joke, but…

Trickz #2

Releasing the GIL

Get speedup from that kind of code:

threads = [Thread(target=pythranized, args=[i])
           for i in range(1, thread_count)]
for thread in threads:
    thread.start()
for thread in threads:
    thread.join()

Trickz #3

Jupyter Integration

Pythran magic cell:

%%pythran -O3
import numpy as np
def arc_distance(theta_1, phi_1, theta_2, phi_2):
    temp = (np.sin((theta_2-theta_1)/2)**2
           + np.cos(theta_1)*np.cos(theta_2) * np.sin((phi_2-phi_1)/2)**2)
    distance_matrix = 2 * np.arctan2(np.sqrt(temp), np.sqrt(1-temp))
    return distance_matrix

Trickz #4

Fancy Indexing and the likes

Pythran supports

Lazy evaluation (incl. for np.where
Broadcasting
Expression Broadcasting (overhead there)
<ufunc>.accumulate

Benchmarks

https://github.com/serge-sans-paille/numpy-benchmarks
A collection of high-level benchmarks

Code gathered from StackOverflow + other compiler code base
Mostly high-level code
Generate results for CPython, PyPy, Numba, Parakeet, Hope and Pythran

Most kernels are too high level for Numba and Hope…

Benchmarks

no parallelism, no vectorisation (, no fat)

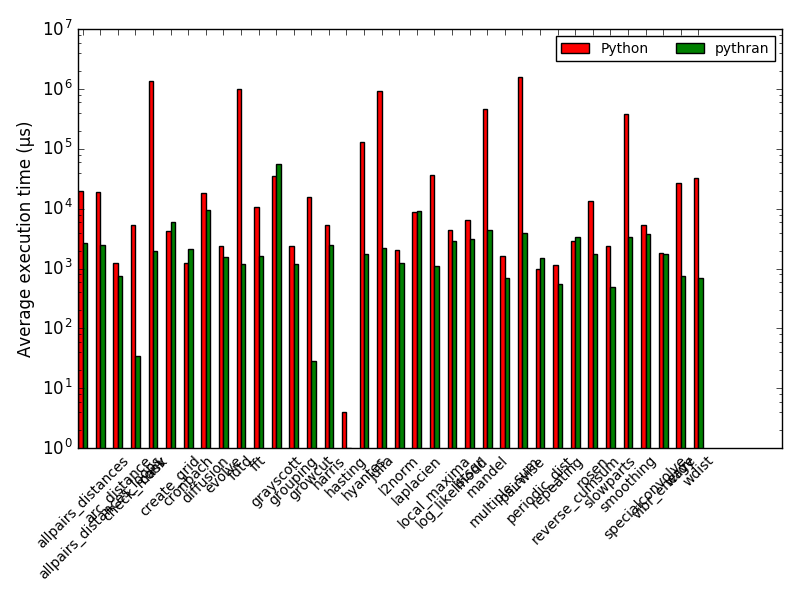
(Num)Focus: growcut

From the Numba codebase!

#pythran export growcut(float[][][], float[][][], float[][][], int)
import math
import numpy as np
def window_floor(idx, radius):
    if radius > idx:
        return 0
    else:
        return idx - radius


def window_ceil(idx, ceil, radius):
    if idx + radius > ceil:
        return ceil
    else:
        return idx + radius

def growcut(image, state, state_next, window_radius):
    changes = 0
    sqrt_3 = math.sqrt(3.0)

    height = image.shape[0]
    width = image.shape[1]

    for j in xrange(width):
        for i in xrange(height):

            winning_colony = state[i, j, 0]
            defense_strength = state[i, j, 1]

            for jj in xrange(window_floor(j, window_radius),
                             window_ceil(j+1, width, window_radius)):
                for ii in xrange(window_floor(i, window_radius),
                                 window_ceil(i+1, height, window_radius)):
                    if (ii != i and jj != j):
                        d = image[i, j, 0] - image[ii, jj, 0]
                        s = d * d
                        for k in range(1, 3):
                            d = image[i, j, k] - image[ii, jj, k]
                            s += d * d
                        gval = 1.0 - math.sqrt(s)/sqrt_3

                        attack_strength = gval * state[ii, jj, 1]

                        if attack_strength > defense_strength:
                            defense_strength = attack_strength
                            winning_colony = state[ii, jj, 0]
                            changes += 1

            state_next[i, j, 0] = winning_colony
            state_next[i, j, 1] = defense_strength

    return changes

(Num)Focus: growcut

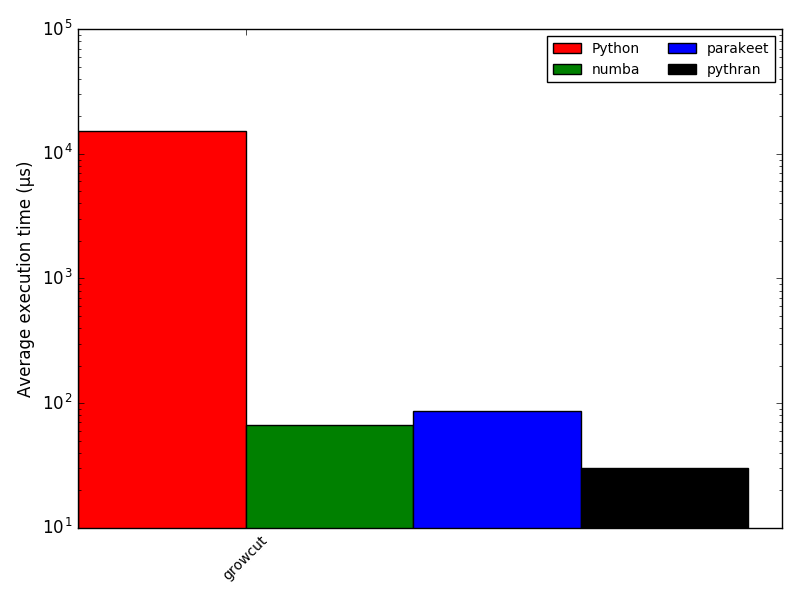
Remember BoB?

(Num)Focus: arc_distance

That's some number crunching!

#pythran export arc_distance(float64 [], float64[],
#                            float64[], float64[])
import numpy as np
def arc_distance(theta_1, phi_1, theta_2, phi_2):
    tmp = (np.sin((theta_2-theta_1)/2)**2 +
           np.cos(theta_1)*np.cos(theta_2)*np.sin((phi_2-phi_1)/2)**2)
    distance_matrix = 2 * (np.arctan2(np.sqrt(tmp),np.sqrt(1-tmp)))
    return distance_matrix

(Num)Focus: arc_distance

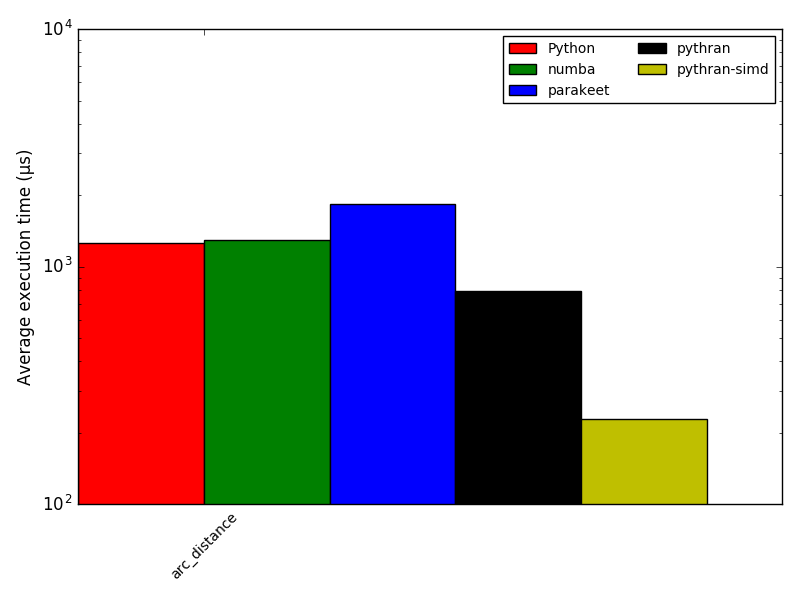
Academic Results

Pythran: Enabling Static Optimization of Scientific Python Programs, S. Guelton, P. Brunet et al. in CSD, 2015
Exploring the Vectorization of Python Constructs Using Pythran and Boost SIMD, S. Guelton, J. Falcou and P. Brunet, in WPMVP, 2014
Compiling Python modules to native parallel modules using Pythran and OpenMP Annotations, S. Guelton, P. Brunet and M. Amini, in PyHPC, 2013
Pythran: Enabling Static Optimization of Scientific Python Programs, S. Guelton, P. Brunet et al. in SciPy, 2013

Powered by Tireless Engineering

Preprequisite for reproductible science

2772 test cases, incl. unit testing, doctest, Continuous integration (thx Travis!)
Various flag/compiler combination tested
Peer-reviewed code
Python2.7 and Python3.6, C++11
Linux, OSX (almost okay), Windows (through WinPython)
User and Developer doc: http://pythonhosted.org/pythran/
Hosted on https://github.com/serge-sans-paille/pythran
Releases on PyPi: $ pip install pythran

We need more peons

Report performance bugs!
numpy.random and numpy.linalg

THE END

AUTHORS: Serge Guelton, Pierrick Brunet + TB Student + Contributors
INDUSTRIAL SUPPORT: Silkan, NumScale, OpenDreamKit →You←
CONTRIBUTE: #pythran on FreeNode, pythran@freelists.org, GitHub repo