Benchmarking Before the Release
This blogpost originally was a Jupyter Notebook. You can download it if you want. The conversion was done using nbconvert and a custom template to match the style of the other part of the blog.
The goal of this notebook is to look for performance regression in Pythran before its release. To do so, several cython kernels have been collected on the World Wide Web, mostly from stackoverflow and blogs.
For each kernel, a Numpy version, a Cython version and a Pythran version (which aims to be equal to the Numpy version, with an additional #pythran export) are benchmarked. If Pythran can rip the same performance level as Cython from the Numpy -like code, then it's ok for the release!
Disclaimer
Benchmarking is a difficult task. This notebook does not aim to be a reference comparison between Cython and Pythran. So many factors are involved: the developper proficiency in Cython, Numpy and Pythran, the underlying C compiler, or C++ compiler (we made sure they were using the same gcc version, at least), their respective compilation flags (they are different, but both use -O2 and not -ffast-math), the Pythran/Cython version… So take it as it is: a way to make sure the Pythran developpers did not miss an obvious optimization opportunity, or introduced a performance regression. No other conclusions should be made without great care.
Setup
The happy few:
>>> import numpy as np
>>> %load_ext Cython
>>> %load_ext pythran.magic
The benchmarking routine:
>>> import timeit
>>> import pandas
>>> from collections import OrderedDict
>>> %matplotlib inline
>>> def run_bench(functions, sizes, args_factory):
... global function, args # to please timeit
... scores = pandas.DataFrame(data=0, columns=functions.keys(), index=sizes)
... for size in sizes:
... size = int(size)
... for name, function in functions.items():
... args = args_factory(size)
... result = %timeit -q -o function(*args)
... scores.loc[size, name] = result.best
... return scores
cos_norm
source: stackoverflow
This kernel tests classical element wise operations à la Numpy.
>>> def np_cos_norm(a, b):
... val = np.sum(1. - np.cos(a-b))
... return np.sqrt(val / 2. / a.shape[0])
>>> %%cython
...
>>> cimport cython
>>> cimport numpy as np
...
>>> cdef extern from "math.h":
... double cos(double x) nogil
... double sqrt(double x) nogil
...
>>> def cython_cos_norm(a, b):
... return cos_norm_impl(a, b)
...
>>> @cython.boundscheck(False)
>>> @cython.wraparound(False)
>>> @cython.cdivision(True)
>>> cdef double cos_norm_impl(double[::1] a, double[::1] b) nogil:
... cdef double res = 0., val
... cdef int m = a.shape[0]
... # XXX: shape of b not checked
... cdef int j
...
... for j in range(m):
... val = a[j] - b[j]
... res += 1. - cos(val)
... res /= 2.*m
...
... return sqrt(res)
>>> %%pythran
...
>>> #pythran export pythran_cos_norm(float[], float[])
>>> import numpy as np
>>> def pythran_cos_norm(a, b):
... val = np.sum(1. - np.cos(a-b))
... return np.sqrt(val / 2. / a.shape[0])
Timings (lower is better)
>>> cos_norms = OrderedDict([('numpy', np_cos_norm),
... ('cython', cython_cos_norm),
... ('pythran', pythran_cos_norm)])
>>> sizes = 1e3, 1e4, 1e5, 1e6
>>> def args_factory(size):
... return (np.random.random(size).astype('float64'),
... np.random.random(size).astype('float64'))
>>> scores = run_bench(cos_norms, sizes, args_factory)
>>> scores.plot()
<matplotlib.axes._subplots.AxesSubplot at 0x7fa4eb26c2d0>
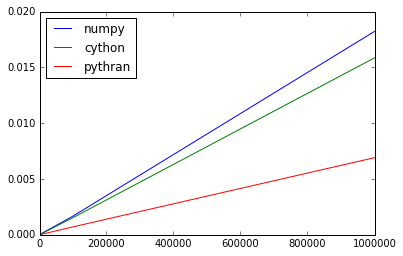
That's unexpected! The reason why we go faster than Cython is the cos routine, as we use nt2 implementation that proves to be very efficient (it has a few shortpaths). Switching back to std::cos gives the same execution time has Cython.
Grayscott
source: stackoverflow
This kernel tests complex array interactions: slices, element-wise operations, everything into a regular loop!
>>> def np_grayscott(counts, Du, Dv, F, k):
... n = 300
... U = np.zeros((n+2,n+2), dtype=np.float_)
... V = np.zeros((n+2,n+2), dtype=np.float_)
... u, v = U[1:-1,1:-1], V[1:-1,1:-1]
...
... r = 20
... u[:] = 1.0
... U[n/2-r:n/2+r,n/2-r:n/2+r] = 0.50
... V[n/2-r:n/2+r,n/2-r:n/2+r] = 0.25
... u += 0.15*np.random.random((n,n))
... v += 0.15*np.random.random((n,n))
...
... for i in range(counts):
... Lu = ( U[0:-2,1:-1] +
... U[1:-1,0:-2] - 4*U[1:-1,1:-1] + U[1:-1,2:] +
... U[2: ,1:-1] )
... Lv = ( V[0:-2,1:-1] +
... V[1:-1,0:-2] - 4*V[1:-1,1:-1] + V[1:-1,2:] +
... V[2: ,1:-1] )
... uvv = u*v*v
... u += Du*Lu - uvv + F*(1 - u)
... v += Dv*Lv + uvv - (F + k)*v
...
... return V
>>> %%cython
...
>>> cimport cython
>>> import numpy as np
>>> cimport numpy as np
...
>>> @cython.boundscheck(False)
>>> @cython.wraparound(False)
>>> @cython.cdivision(True)
>>> cpdef cython_grayscott(int counts, double Du, double Dv, double F, double k):
... cdef int n = 300
... cdef np.ndarray U = np.zeros((n+2,n+2), dtype=np.float_)
... cdef np.ndarray V = np.zeros((n+2,n+2), dtype=np.float_)
... cdef np.ndarray u = U[1:-1,1:-1]
... cdef np.ndarray v = V[1:-1,1:-1]
...
... cdef int r = 20
... u[:] = 1.0
... U[n/2-r:n/2+r,n/2-r:n/2+r] = 0.50
... V[n/2-r:n/2+r,n/2-r:n/2+r] = 0.25
... u += 0.15*np.random.random((n,n))
... v += 0.15*np.random.random((n,n))
...
... cdef np.ndarray Lu = np.zeros_like(u)
... cdef np.ndarray Lv = np.zeros_like(v)
... cdef int i, c, r1, c1, r2, c2
... cdef double uvv
...
... cdef double[:, ::1] bU = U
... cdef double[:, ::1] bV = V
... cdef double[:, ::1] bLu = Lu
... cdef double[:, ::1] bLv = Lv
...
... for i in range(counts):
... for r in range(n):
... r1 = r + 1
... r2 = r + 2
... for c in range(n):
... c1 = c + 1
... c2 = c + 2
... bLu[r,c] = bU[r1,c2] + bU[r1,c] + bU[r2,c1] + bU[r,c1] - 4*bU[r1,c1]
... bLv[r,c] = bV[r1,c2] + bV[r1,c] + bV[r2,c1] + bV[r,c1] - 4*bV[r1,c1]
...
... for r in range(n):
... r1 = r + 1
... for c in range(n):
... c1 = c + 1
... uvv = bU[r1,c1]*bV[r1,c1]*bV[r1,c1]
... bU[r1,c1] += Du*bLu[r,c] - uvv + F*(1 - bU[r1,c1])
... bV[r1,c1] += Dv*bLv[r,c] + uvv - (F + k)*bV[r1,c1]
...
... return V
>>> %%pythran
...
>>> #pythran export pythran_grayscott(int, float, float, float, float)
>>> import numpy as np
>>> def pythran_grayscott(counts, Du, Dv, F, k):
... n = 300
... U = np.zeros((n+2,n+2), dtype=np.float_)
... V = np.zeros((n+2,n+2), dtype=np.float_)
... u, v = U[1:-1,1:-1], V[1:-1,1:-1]
...
... r = 20
... u[:] = 1.0
... U[n/2-r:n/2+r,n/2-r:n/2+r] = 0.50
... V[n/2-r:n/2+r,n/2-r:n/2+r] = 0.25
... u += 0.15*np.random.random((n,n))
... v += 0.15*np.random.random((n,n))
...
... for i in range(counts):
... Lu = ( U[0:-2,1:-1] +
... U[1:-1,0:-2] - 4*U[1:-1,1:-1] + U[1:-1,2:] +
... U[2: ,1:-1] )
... Lv = ( V[0:-2,1:-1] +
... V[1:-1,0:-2] - 4*V[1:-1,1:-1] + V[1:-1,2:] +
... V[2: ,1:-1] )
... uvv = u*v*v
... u += Du*Lu - uvv + F*(1 - u)
... v += Dv*Lv + uvv - (F + k)*v
...
... return V
Timings (lower is better)
>>> grayscotts = OrderedDict([('numpy', np_grayscott),
... ('cython', cython_grayscott),
... ('pythran', pythran_grayscott)])
>>> sizes = 1e1, 5e1, 1e2, 5e2, 1e3
>>> def args_factory(size):
... return size, 0.16, 0.08, 0.04, 0.06
>>> scores = run_bench(grayscotts, sizes, args_factory)
>>> scores.plot()
<matplotlib.axes._subplots.AxesSubplot at 0x7fa4e5f8ff10>
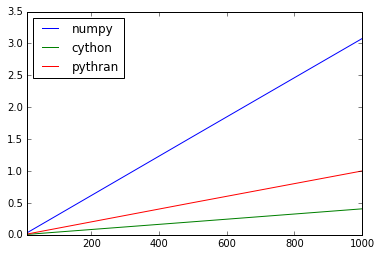
We have a small issue there. Need to investigate! Still a decent speedup though.
clip
source: pythran issue
This kernel tests conditionnal assignment (through np.where) and array of complex numbers.
>>> def np_clip(z, _max):
... return np.where(np.abs(z) > _max, z/np.abs(z) * _max, z)
>>> %%cython
...
>>> cimport cython
>>> import numpy as np
>>> cimport numpy as np
...
>>> cdef extern from "complex.h":
... double cabs(double complex x) nogil
...
>>> @cython.boundscheck(False)
>>> @cython.wraparound(False)
>>> @cython.cdivision(True)
>>> cpdef cython_clip (double complex[::1] z, double _max):
... cdef np.ndarray out_ = np.empty_like(z)
... cdef int n = len(z), i
... cdef double complex[::1] out = out_
... for i in range (n):
... if cabs(z[i]) > _max:
... out[i] = z[i]/cabs(z[i]) * _max
... else:
... out[i] = z[i]
...
... return out
>>> %%pythran
...
>>> #pythran export pythran_clip(complex128[], float64)
>>> import numpy as np
>>> def pythran_clip(z, _max):
... return np.where(np.abs(z) > _max, z/np.abs(z) * _max, z)
Timings (lower is better)
>>> clips = OrderedDict([('numpy', np_clip),
... ('cython', cython_clip),
... ('pythran', pythran_clip)])
>>> sizes = 1e2, 1e3, 1e4, 1e5, 1e6
>>> def args_factory(size):
... return np.arange(size, dtype=complex) * complex(1,1), size/2
>>> scores = run_bench(clips, sizes, args_factory)
>>> scores.plot()
<matplotlib.axes._subplots.AxesSubplot at 0x7fa4eb4e8990>
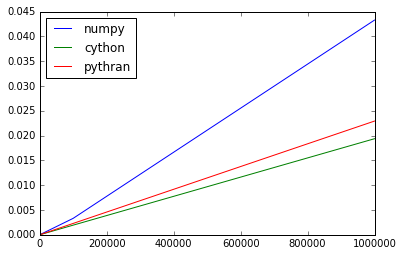
Nice! Brest! Slightly worse than Cython, but we could improve this by implementing common subexpression elimination at the array level.
Pariwise distance
sources: jakevdp blog and Anaconda blog
This kernel tests Numpy's broadcasting.
>>> def np_pairwise(X):
... return np.sqrt(((X[:, None, :] - X) ** 2).sum(-1))
>>> %%cython
...
>>> import numpy as np
>>> cimport cython
>>> from libc.math cimport sqrt
...
>>> @cython.boundscheck(False)
>>> @cython.wraparound(False)
>>> def cython_pairwise(double[:, ::1] X):
... cdef int M = X.shape[0]
... cdef int N = X.shape[1]
... cdef double tmp, d
... cdef double[:, ::1] D = np.empty((M, M), dtype=np.float64)
... for i in range(M):
... for j in range(M):
... d = 0.0
... for k in range(N):
... tmp = X[i, k] - X[j, k]
... d += tmp * tmp
... D[i, j] = sqrt(d)
... return np.asarray(D)
>>> %%pythran
...
>>> #pythran export pythran_pairwise(float64 [][])
>>> import numpy as np
>>> def pythran_pairwise(X):
... return np.sqrt(((X[:, None, :] - X) ** 2).sum(-1))
Timings
>>> pairwises = OrderedDict([('numpy', np_pairwise),
... ('cython', cython_pairwise),
... ('pythran', pythran_pairwise)])
>>> sizes = 0.5e2, 1e2, 2.5e2, 5e2
>>> def args_factory(size):
... return np.random.random((size, size)),
>>> scores = run_bench(pairwises, sizes, args_factory)
>>> scores.plot()
<matplotlib.axes._subplots.AxesSubplot at 0x7fa4eb44ab10>
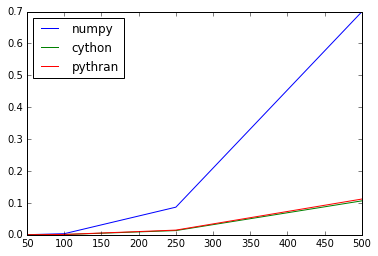
Wooo! Being able to compile this expression down to something that matches Cython's generated code is an achivement :-)
lu factorization
source: jfp blog
This kernel tests interaction between Numpy arrays, slices and regular loops.
>>> def np_det_by_lu(y, x):
... y[0] = 1.
...
... N = x.shape[0]
... with np.errstate(invalid='ignore'):
... for k in range(N):
... y[0] *= x[k,k]
... xk = x[k]
... for i in range(k+1, N):
... xi = x[i]
... xi[k] /= xk[k]
... xi[k+1:] -= xi[k] * xk[k+1:]
...
...
>>> %%cython
...
>>> import cython
...
>>> @cython.boundscheck(False)
>>> @cython.wraparound(False)
>>> cpdef cython_det_by_lu(double[:] y, double[:,:] x):
... y[0] = 1.
...
... cdef int N = x.shape[0]
... cdef int i,j,k
...
... for k in range(N):
... y[0] *= x[k,k]
... for i in range(k+1, N):
... x[i,k] /= x[k,k]
... for j in range(k+1, N):
... x[i,j] -= x[i,k] * x[k,j]
...
...
>>> %%pythran
>>> #pythran export pythran_det_by_lu(float64 [:], float64[:,:])
>>> def pythran_det_by_lu(y, x):
... y[0] = 1.
... N = x.shape[0]
...
... for k in range(N):
... y[0] *= x[k,k]
... xk = x[k]
... for i in range(k+1, N):
... xi = x[i]
... xi[k] /= xk[k]
... xi[k+1:] -= xi[k] * xk[k+1:]
Timings
>>> det_by_lus = OrderedDict([('numpy', np_det_by_lu),
... ('cython', cython_det_by_lu),
... ('pythran', pythran_det_by_lu)])
>>> sizes = 1e2, 2.5e2, 5e2; 7.5e2, 1e3
>>> def args_factory(size):
... return np.random.random(size), np.random.random((size, size))
>>> scores = run_bench(det_by_lus, sizes, args_factory)
>>> scores.plot()
<matplotlib.axes._subplots.AxesSubplot at 0x7fa4eb4b66d0>
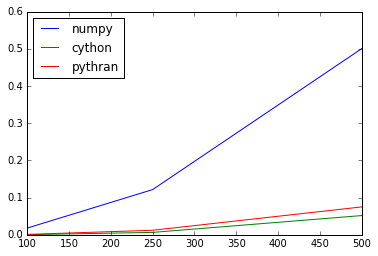
On par with Cython, checked! Note that both Cython and Pythran kernel don't handle errors as Numpy kernel does…
Conclusion
Ready for release? Looks like everything is ok, we're most of the time not far from cython, while keeping the Numpy high-level calls \o/
Acknowledgments
Thanks a lot to the authors of the cited blogs / stackoverflow threads for providing stimulating code samples. I did improve my cython king-fu a lot thanks to you!
(by order of apparition)